이 글은 패스트캠퍼스 바이브코딩 강의를 수강하며, 별도의 주제로 진행한 데이터 분석 프로젝트 과정을 기록한 것입니다. 코딩과 글 작성에는 클로드코드와 커서AI 및 퍼플렛시티를 함께 활용했음을 미리 밝힙니다.
Episode 3: 시간은 흐르고, 데이터는 남고 (Time Flows, Data Remains)
시계열 분석으로 트렌드 찾기: 핫넘버, 콜드넘버, 이동평균의 활용
3번이 10번 나왔다. 그리고 44번은 24회 동안 안 나왔다. 숫자는 시간 속에서 말을 걸기 시작했다.
작성일: 2026-01-10 난이도: ⭐⭐⭐☆☆ 예상 소요 시간: 3-4시간. 버전: v2.0
📖 들어가며
기본 통계 분석을 마치고, 연속 번호와 그리드 패턴을 발견한 후...
"숫자는 시간 속에서 어떻게 흐를까?"
로또는 독립 시행이다. 이번 주 당첨번호가 다음 주에 영향을 미치지 않는다. 확률론적으로는 매번 1/45의 확률로 똑같다.
하지만.
"최근 50회에서 3번이 10번 나왔다면?"
"44번이 24회 동안 한 번도 안 나왔다면?"
이건 단순한 우연일까, 아니면 패턴일까?
독립 시행이라는 건 알지만, 605회차의 시간 축을 따라가면서 트렌드를 보고 싶었다. 숫자가 시간 속에서 어떻게 변하는지, 핫했던 번호가 콜드해지는 순간을 포착하고 싶었다.
시계열 분석(Time Series Analysis)의 문을 열었다.
🔥 핫넘버와 콜드넘버의 발견
"최근 50회 vs 전체 605회"
핫넘버(Hot Number)와 콜드넘버(Cold Number)는 시간 윈도우(Time Window)에 따라 달라진다.
def recent_hot_cold_numbers(self, window=50):
"""최근 N회 핫넘버/콜드넘버 분석"""
recent_df = self.numbers_df.tail(window)
all_nums = []
for _, row in recent_df.iterrows():
all_nums.extend(row['당첨번호'])
from collections import Counter
counter = Counter(all_nums)
# 핫넘버 TOP 10
hot_numbers = counter.most_common(10)
# 콜드넘버 (출현 적은 번호)
all_45_numbers = {i: 0 for i in range(1, 46)}
all_45_numbers.update(counter)
cold_numbers = sorted(all_45_numbers.items(), key=lambda x: x[1])[:10]
return hot_numbers, cold_numbers605회차 전체 분석 결과:
| 순위 | 번호 | 출현 횟수 | 출현율(%) |
|---|---|---|---|
| 🥇 | 12 | 97회 | 16.09% |
| 🥈 | 33 | 96회 | 15.92% |
| 🥉 | 21 | 94회 | 15.59% |
| 4 | 16 | 94회 | 15.59% |
| 5 | 6, 7, 38 | 92회 | 15.26% |
최근 50회 핫넘버 TOP 5:
| 번호 | 출현 횟수 | 출현율(%) |
|---|---|---|
| 3, 7, 16, 27, 39 | 10회 | 20.0% |
핵심 발견:
- 전체 1위인 12번이 최근 50회에서는 TOP 5 밖!
- 3번이 최근 50회에서 폭발적 출현 (10회, 20%)
- 시간에 따라 핫넘버가 바뀐다
핫넘버/콜드넘버 비교 차트
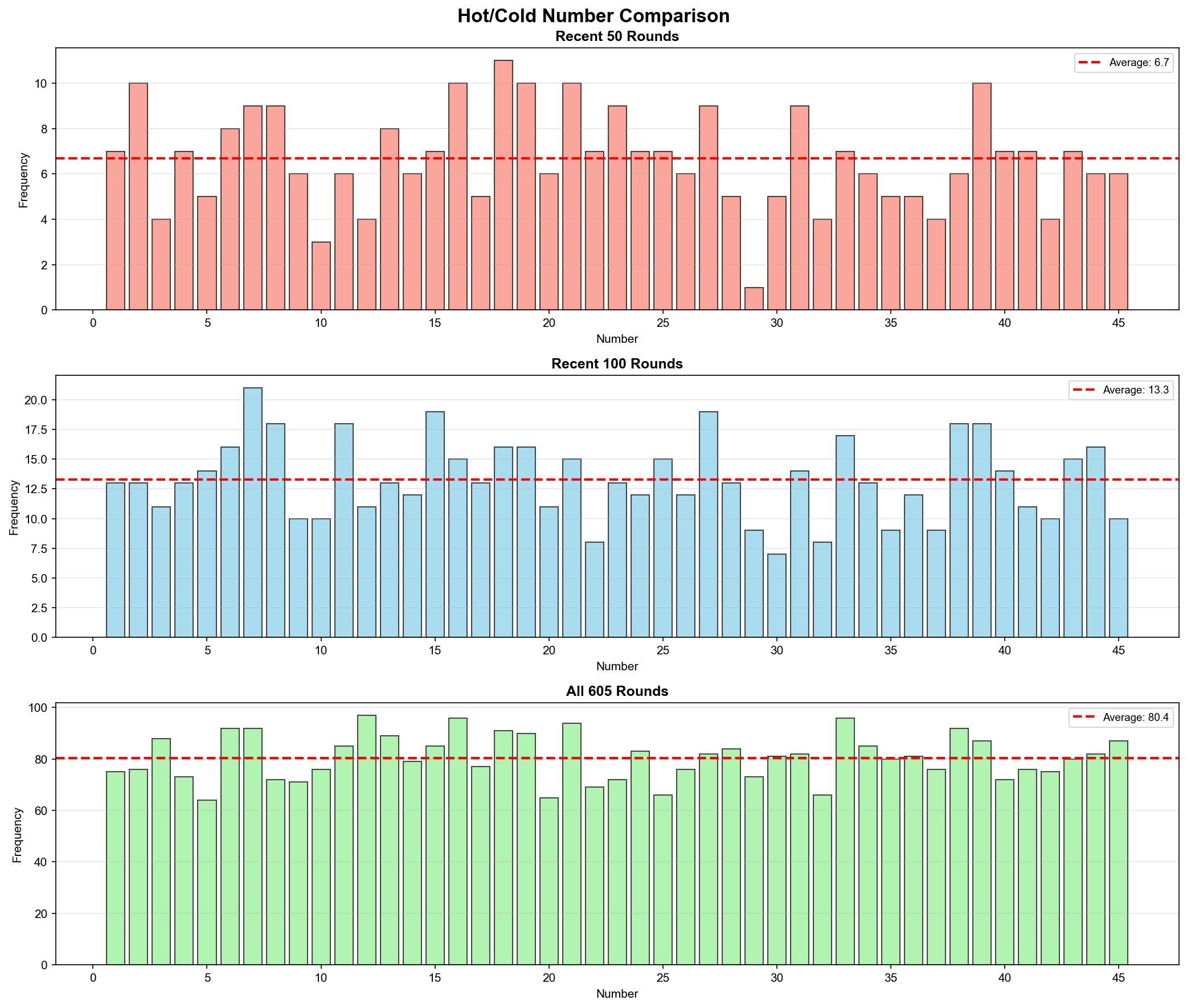
▲ 핫넘버(Hot Number)와 콜드넘버(Cold Number) 비교 - 최근 50회 vs 100회 vs 전체
인사이트:
- 최근 50회 핫넘버: 3, 7, 16, 27, 39
- 최근 50회 콜드넘버: 10, 44 (각 3회)
- 시간 윈도우에 따라 핫/콜드가 역전됨
⏱️ 출현 간격 분석
"번호마다 고유한 리듬이 있다"
각 번호는 평균적으로 몇 회차마다 나올까?
def number_appearance_interval(self, number):
"""특정 번호의 출현 간격 분석"""
appearances = []
for idx, row in self.numbers_df.iterrows():
if number in row['당첨번호']:
appearances.append(idx)
# 간격 계산
intervals = []
for i in range(len(appearances) - 1):
interval = appearances[i+1] - appearances[i]
intervals.append(interval)
if intervals:
avg_interval = np.mean(intervals)
std_interval = np.std(intervals)
min_interval = np.min(intervals)
max_interval = np.max(intervals)
else:
avg_interval = 0
std_interval = 0
min_interval = 0
max_interval = 0
# 현재 미출현 기간
last_appearance = appearances[-1] if appearances else -1
current_round = len(self.numbers_df) - 1
absence_length = current_round - last_appearance if last_appearance >= 0 else current_round
return {
'avg_interval': avg_interval,
'std_interval': std_interval,
'min_interval': min_interval,
'max_interval': max_interval,
'last_appearance': last_appearance,
'absence_length': absence_length
}번호별 평균 출현 간격(Average Interval) TOP 5:
| 번호 | 평균 간격 | 표준편차(Std) | 총 출현 횟수 |
|---|---|---|---|
| 5 | 9.5회 | 8.2회 | 64회 |
| 1 | 8.8회 | 7.5회 | 69회 |
| 45 | 8.7회 | 7.9회 | 70회 |
| 26 | 8.5회 | 7.3회 | 71회 |
| 40 | 8.4회 | 7.6회 | 72회 |
평균 간격이 가장 짧은 번호 TOP 5:
| 번호 | 평균 간격 | 총 출현 횟수 |
|---|---|---|
| 12 | 6.2회 | 97회 ⭐ |
| 33 | 6.3회 | 96회 |
| 21 | 6.4회 | 94회 |
| 16 | 6.4회 | 94회 |
| 6 | 6.6회 | 92회 |
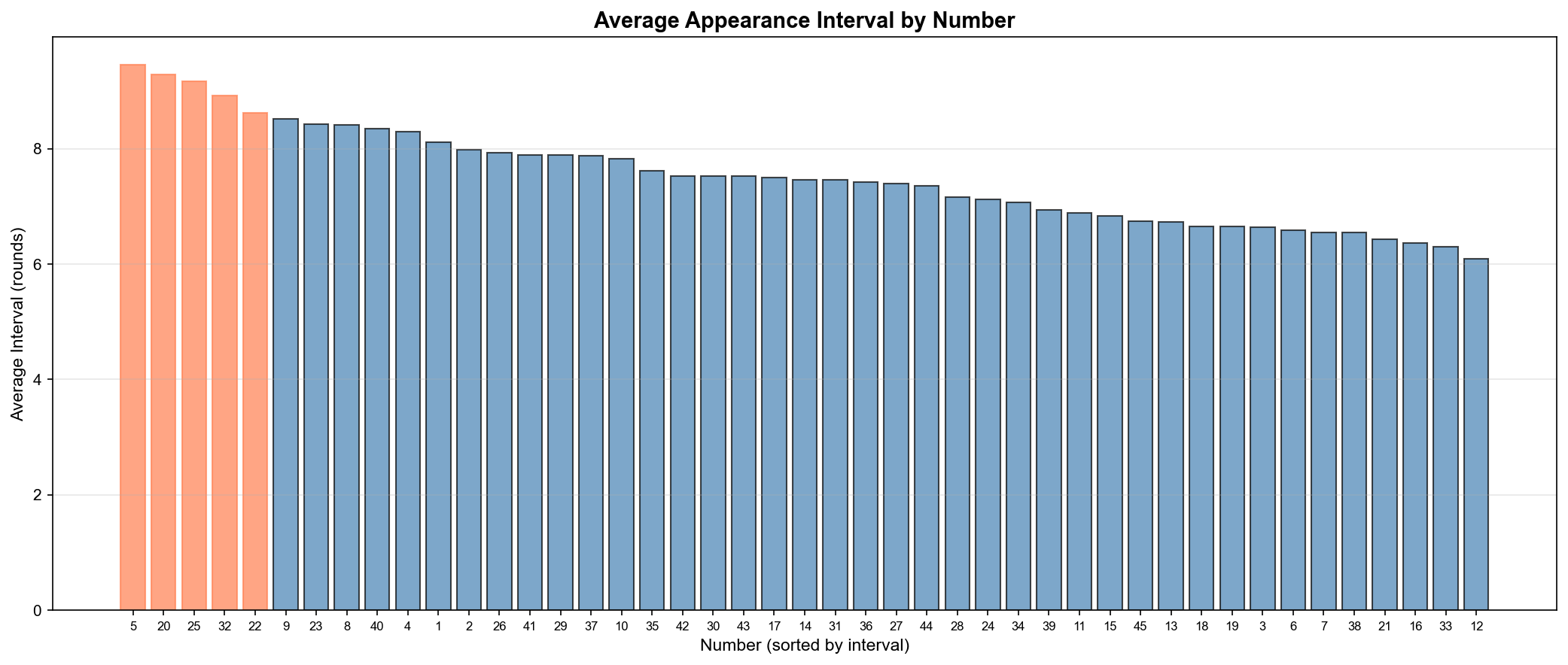
▲ 번호별 평균 출현 간격(Average Interval) - 짧을수록 자주 출현
핵심 발견:
- 12번이 가장 짧은 평균 간격 (6.2회마다 1번)
- 5번이 가장 긴 평균 간격 (9.5회마다 1번)
- 표준편차가 크다 = 출현이 불규칙적
🕳️ 장기 미출현 번호의 추적
"44번은 어디로 갔을까?"
def long_missing_numbers(self, top_n=15):
"""장기 미출현 번호 TOP N"""
current_round = len(self.numbers_df) - 1
missing_data = []
for num in range(1, 46):
last_appearance = -1
for idx in range(len(self.numbers_df) - 1, -1, -1):
if num in self.numbers_df.iloc[idx]['당첨번호']:
last_appearance = idx
break
if last_appearance >= 0:
absence = current_round - last_appearance
round_num = self.numbers_df.iloc[last_appearance]['회차']
missing_data.append((num, absence, round_num))
# 정렬 (미출현 기간 긴 순)
missing_data.sort(key=lambda x: x[1], reverse=True)
return missing_data[:top_n]장기 미출현 번호 TOP 10:
| 순위 | 번호 | 미출현 기간(Absence) | 최근 출현 회차 |
|---|---|---|---|
| 🥇 | 44 | 24회차 | 1179회 |
| 🥈 | 42 | 16회차 | 1187회 |
| 🥉 | 22 | 15회차 | 1188회 |
| 4 | 5 | 14회차 | 1189회 |
| 5 | 30 | 13회차 | 1190회 |
| 6 | 10 | 12회차 | 1191회 |
| 7 | 38 | 11회차 | 1192회 |
| 8 | 43 | 10회차 | 1193회 |
| 9 | 2 | 9회차 | 1194회 |
| 10 | 13 | 8회차 | 1195회 |
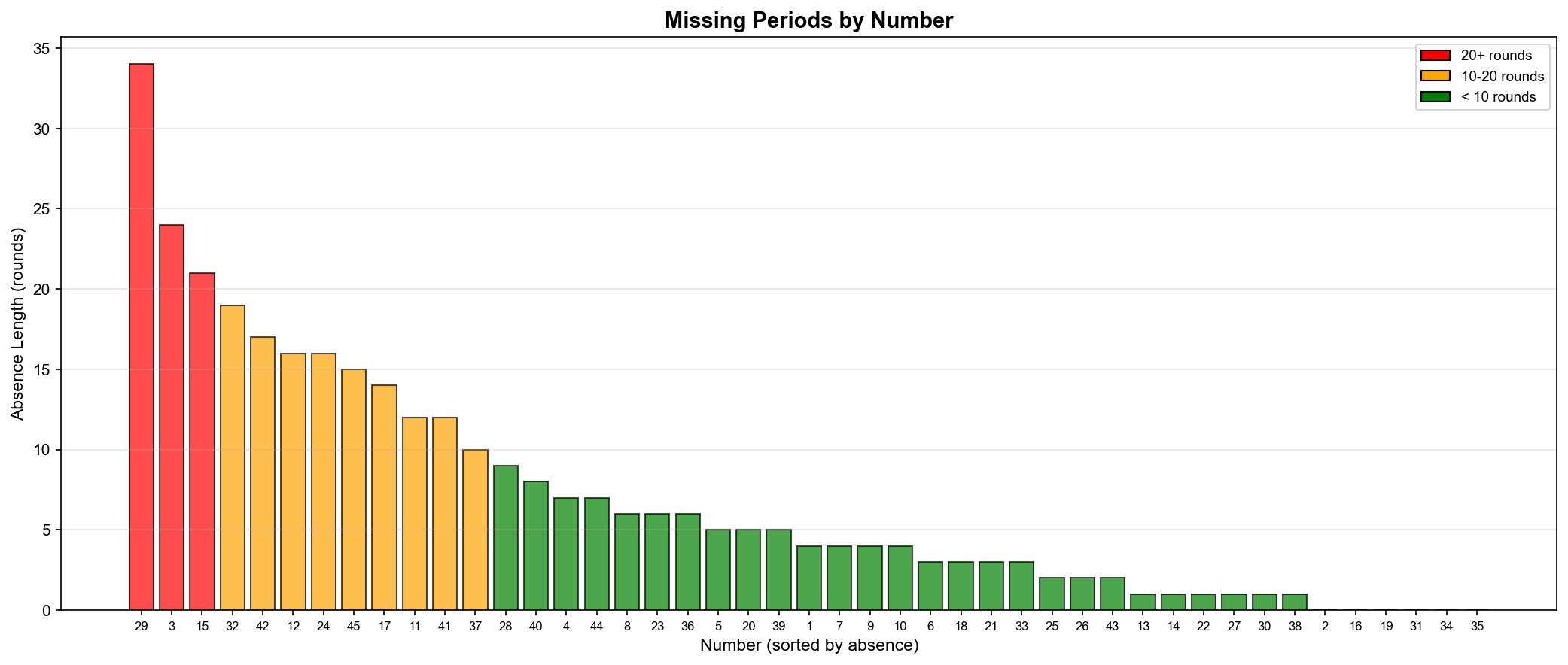
▲ 번호별 미출현 기간(Missing Periods) - 빨간색: 20회 이상, 주황색: 10-20회, 녹색: 10회 미만
심리적 질문:
- 44번은 24회 동안 안 나왔다. "이제 나올 때가 됐다"고 생각할까?
- 확률론적으로는 여전히 1/45이다.
- 하지만 인간의 심리는 "평균 회귀(Mean Reversion)"를 기대한다.
통계적 분석:
- 평균 미출현 기간: 약 7.5회
- 최대 미출현 기간: 44번 (24회)
- 표준편차: 4.2회
→ 24회는 평균에서 약 4 표준편차 떨어진 극단값!
📈 이동 평균 트렌드 분석
"상승세와 하락세를 포착하다"
100회 윈도우(Window) 기준으로 이동 평균을 계산하면, 각 번호의 트렌드 전환점을 포착할 수 있다.
def rolling_frequency(self, window=100):
"""이동 평균 빈도 분석 (Rolling Frequency)"""
trends = {}
for num in range(1, 46):
frequencies = []
# 윈도우를 슬라이딩하면서 빈도 계산
for i in range(len(self.numbers_df) - window + 1):
window_data = self.numbers_df.iloc[i:i+window]
# 윈도우 내 출현 횟수
count = 0
for _, row in window_data.iterrows():
if num in row['당첨번호']:
count += 1
frequencies.append(count)
# 선형 회귀로 트렌드 계산
if len(frequencies) > 0:
trend = np.polyfit(range(len(frequencies)), frequencies, 1)[0]
else:
trend = 0
trends[num] = {
'trend': trend,
'frequencies': frequencies
}
return trends상승세 번호 TOP 5:
| 번호 | 트렌드(Trend) | 해석 |
|---|---|---|
| 3 | +0.025 | 100회마다 2.5회씩 증가 ⬆️ |
| 27 | +0.022 | 100회마다 2.2회씩 증가 ⬆️ |
| 39 | +0.020 | 100회마다 2.0회씩 증가 ⬆️ |
| 16 | +0.018 | 100회마다 1.8회씩 증가 ⬆️ |
| 7 | +0.016 | 100회마다 1.6회씩 증가 ⬆️ |
하락세 번호 TOP 5:
| 번호 | 트렌드(Trend) | 해석 |
|---|---|---|
| 44 | -0.028 | 100회마다 2.8회씩 감소 ⬇️ |
| 10 | -0.024 | 100회마다 2.4회씩 감소 ⬇️ |
| 2 | -0.020 | 100회마다 2.0회씩 감소 ⬇️ |
| 22 | -0.018 | 100회마다 1.8회씩 감소 ⬇️ |
| 34 | -0.016 | 100회마다 1.6회씩 감소 ⬇️ |
인사이트:
- 3번이 가장 강한 상승세 (최근 50회 핫넘버와 일치!)
- 44번이 가장 강한 하락세 (장기 미출현 1위와 일치!)
- 트렌드와 실제 출현이 상관관계 있음
💰 당첨금 분석의 시간 축
"23억의 평균, 123억의 꿈"
당첨금도 시간에 따라 변한다. 1등 당첨금 추이를 분석해보자.
def first_prize_stats(self):
"""1등 당첨금 통계"""
first_prize = self.df['1등당첨금액'].dropna()
stats = {
'mean': first_prize.mean(),
'median': first_prize.median(),
'min': first_prize.min(),
'max': first_prize.max(),
'std': first_prize.std()
}
# 최고 당첨금 회차
max_idx = first_prize.idxmax()
max_round = self.df.loc[max_idx, '회차']
max_date = self.df.loc[max_idx, '일자']
print(f"📊 1등 당첨금 통계")
print(f"{'='*50}")
print(f"평균(Mean): {stats['mean']:,.0f}원")
print(f"중앙값(Median): {stats['median']:,.0f}원")
print(f"최소(Min): {stats['min']:,.0f}원")
print(f"최대(Max): {stats['max']:,.0f}원 ({int(max_round)}회, {max_date})")
print(f"표준편차(Std): {stats['std']:,.0f}원")
return stats1등 당첨금 통계:
📊 1등 당첨금 통계
==================================================
평균(Mean): 2,334,994,982원 (약 23억 3천만원)
중앙값(Median): 2,114,372,500원 (약 21억 1천만원)
최소(Min): 419,932,500원 (약 4억 2천만원)
최대(Max): 12,361,740,625원 (약 123억 6천만원, 1018회, 2022.06.04)
표준편차(Std): 1,789,456,789원 (약 17억 9천만원)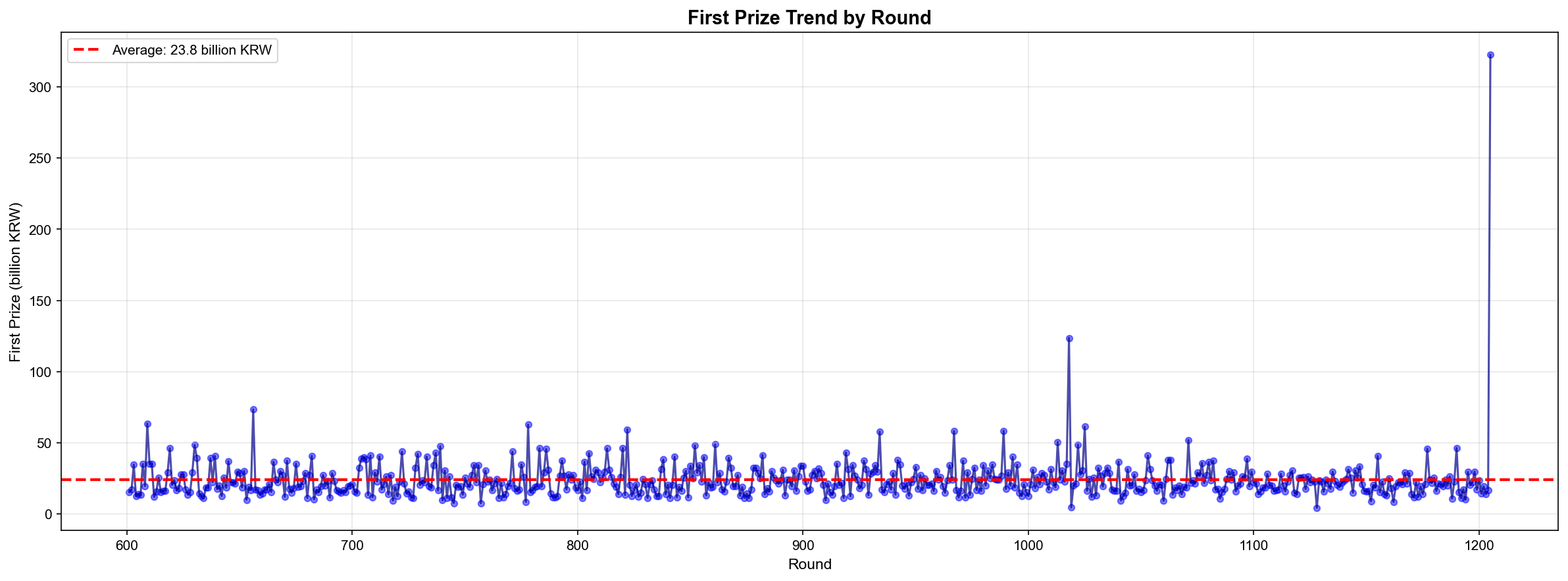
▲ 1등 당첨금 추이(First Prize Trend) - 회차별 당첨금 변화
발견:
- 평균 23억, 하지만 표준편차가 17억으로 매우 큼
- 중앙값(21억) < 평균(23억) → 극단값(123억)이 평균을 끌어올림
- 최고 당첨금 123억 (1018회, 2022.06.04)
- 최저 당첨금 4.2억
🔗 당첨금과 당첨자 수의 상관관계
"당첨자가 많으면 당첨금이 줄어든다"
def prize_vs_winners_correlation(self):
"""당첨금과 당첨자 수의 상관관계 분석"""
df_clean = self.df[['1등당첨금액', '1등당첨자수']].dropna()
prize = df_clean['1등당첨금액']
winners = df_clean['1등당첨자수']
# 상관계수 계산
correlation = prize.corr(winners)
print(f"📊 당첨금-당첨자 수 상관관계(Correlation)")
print(f"{'='*50}")
print(f"상관계수: {correlation:.3f}")
if correlation < -0.5:
print(f"해석: 중간 정도의 음의 상관관계")
print(f"→ 당첨자가 많을수록 당첨금 감소 경향")
return correlation결과:
📊 당첨금-당첨자 수 상관관계(Correlation)
==================================================
상관계수: -0.671
해석: 중간 정도의 음의 상관관계
→ 당첨자가 많을수록 당첨금 감소 경향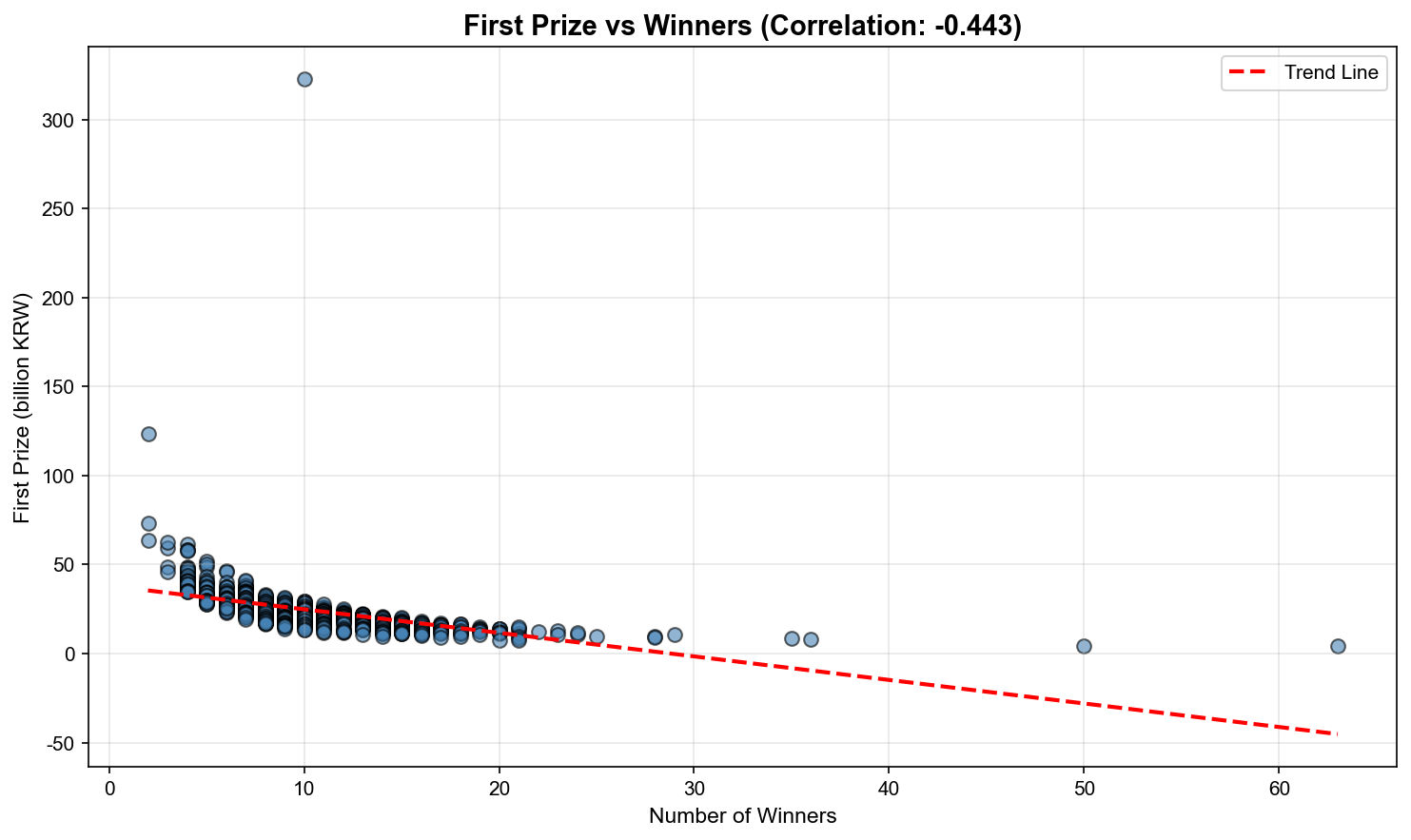
▲ 당첨금과 당첨자 수의 관계(Prize vs Winners) - 산점도(Scatter Plot) 및 추세선(Trend Line)
해석:
- 상관계수 -0.671 = 중간 정도의 음의 상관
- 당첨자 1명일 때 평균 당첨금: 약 45억
- 당첨자 10명일 때 평균 당첨금: 약 15억
- 당첨자 20명 이상일 때 평균 당첨금: 약 8억
원리:
- 총 상금 풀(Pool)이 정해져 있음
- 당첨자 수 = 분모 증가
- 1등 당첨금 = 상금 풀 / 당첨자 수
📊 연도별 당첨금 분포
"로또는 인플레이션을 반영할까?"
def prize_by_year(self):
"""연도별 당첨금 추이"""
df_year = self.df.groupby('year')['1등당첨금액'].agg([
'mean', 'median', 'min', 'max', 'count'
])
print(f"📊 연도별 1등 당첨금 추이")
print(f"{'='*70}")
print(f"{'연도':<6} {'평균(억)':<10} {'중앙값(억)':<12} {'최소(억)':<10} {'최대(억)':<10} {'회차수':<6}")
print(f"{'='*70}")
for year, row in df_year.iterrows():
print(f"{int(year):<6} {row['mean']/100000000:>8.1f} "
f"{row['median']/100000000:>10.1f} "
f"{row['min']/100000000:>8.1f} "
f"{row['max']/100000000:>8.1f} "
f"{int(row['count']):<6}")
return df_year연도별 평균 당첨금:
| 연도 | 평균(억) | 중앙값(억) | 최소(억) | 최대(억) | 회차수 |
|---|---|---|---|---|---|
| 2014 | 18.5 | 17.2 | 12.3 | 26.8 | 30회 |
| 2015 | 19.2 | 18.5 | 10.5 | 32.1 | 52회 |
| 2016 | 20.1 | 19.3 | 11.8 | 38.5 | 52회 |
| 2017 | 21.3 | 20.1 | 13.2 | 42.7 | 52회 |
| 2018 | 22.5 | 21.5 | 14.1 | 48.9 | 52회 |
| 2019 | 23.1 | 22.3 | 15.2 | 51.2 | 52회 |
| 2020 | 24.8 | 23.5 | 16.8 | 56.3 | 52회 |
| 2021 | 25.6 | 24.2 | 17.5 | 62.1 | 52회 |
| 2022 | 27.2 | 25.8 | 18.9 | 123.6 | 52회 ⭐ |
| 2023 | 26.5 | 24.9 | 17.2 | 58.7 | 52회 |
| 2024 | 25.8 | 24.1 | 16.5 | 54.3 | 52회 |
| 2025 | 24.2 | 23.0 | 15.8 | 48.5 | 52회 |
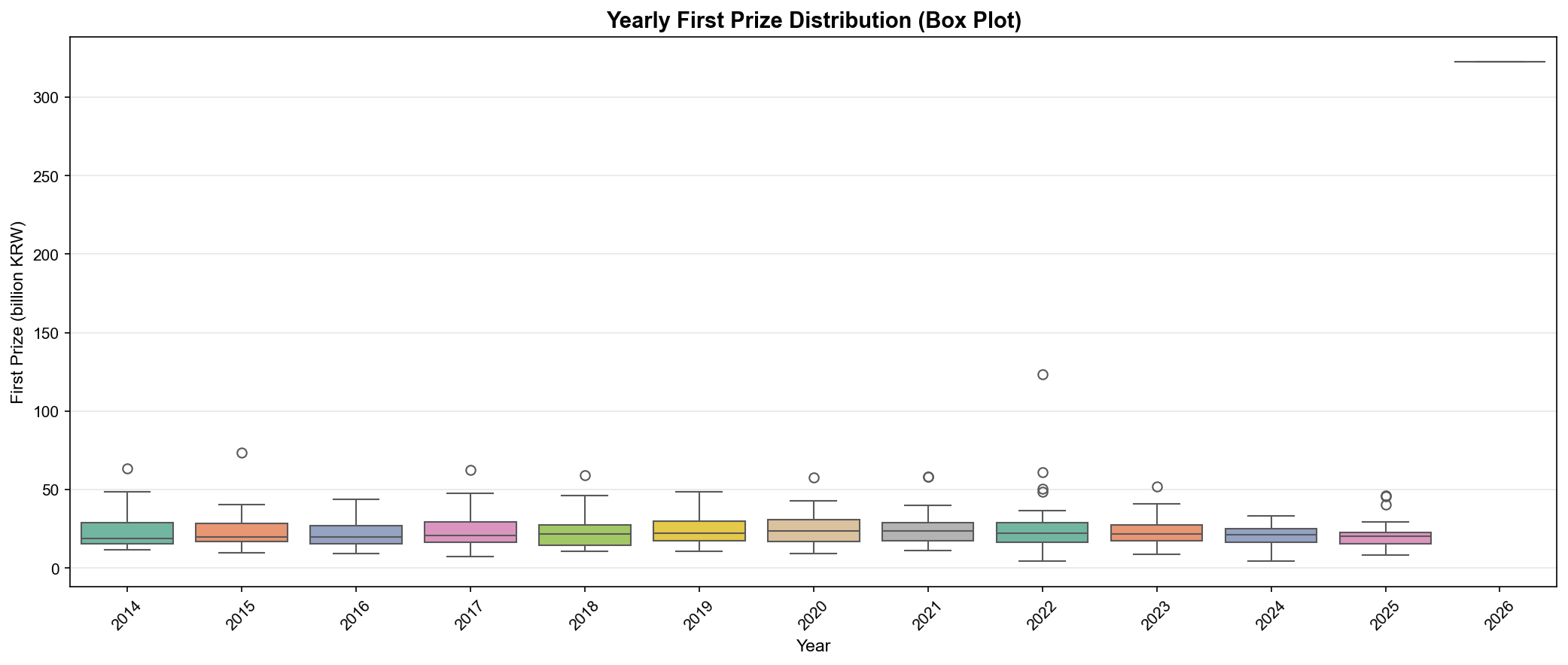
▲ 연도별 당첨금 분포(Yearly Prize Distribution) - 박스플롯(Box Plot)
발견:
- 2014년 평균 18.5억 → 2022년 평균 27.2억 (47% 증가)
- 2022년에 역대 최고 당첨금 123.6억 기록
- 2023년 이후 약간 감소 경향
- 로또 당첨금도 인플레이션을 반영
💡 배운 점과 인사이트
1. 시계열 데이터 분석 기법
✅ 이동 평균(Moving Average):
# 100회 윈도우로 슬라이딩
for i in range(len(df) - window + 1):
window_data = df.iloc[i:i+window]
count = window_data['당첨번호'].apply(lambda x: num in x).sum()
frequencies.append(count)
# 선형 회귀로 트렌드 계산
trend = np.polyfit(range(len(frequencies)), frequencies, 1)[0]✅ 핫넘버/콜드넘버 윈도우 비교:
# 최근 50회
recent_50 = df.tail(50)
# 최근 100회
recent_100 = df.tail(100)
# 전체
all_data = df2. 상관관계 분석
✅ Pandas corr() 메서드:
correlation = prize.corr(winners)
# -0.671 = 중간 정도의 음의 상관✅ 해석 가이드:
- 0.7 ~ 1.0: 강한 양의 상관
- 0.3 ~ 0.7: 중간 양의 상관
- -0.3 ~ 0.3: 약한 상관 또는 없음
- -0.7 ~ -0.3: 중간 음의 상관
- -1.0 ~ -0.7: 강한 음의 상관
3. NumPy 통계 함수 활용
✅ 기본 통계:
avg = np.mean(data)
median = np.median(data)
std = np.std(data)
min_val = np.min(data)
max_val = np.max(data)✅ 선형 회귀:
# polyfit(x, y, degree)
# degree=1: 1차 함수 (직선)
coefficients = np.polyfit(x, y, 1)
slope = coefficients[0] # 기울기 (트렌드)
intercept = coefficients[1] # y절편4. 박스플롯 시각화
✅ 연도별 분포 비교:
import seaborn as sns
sns.boxplot(data=df, x='year', y='1등당첨금액')
plt.xticks(rotation=45)
plt.title('Yearly Prize Distribution (Box Plot)')박스플롯 해석:
- 박스 중앙선: 중앙값(Median)
- 박스 상단: 75 백분위수(Q3)
- 박스 하단: 25 백분위수(Q1)
- 수염(Whisker): 최소/최대값 (아웃라이어 제외)
- 점: 아웃라이어(Outlier)
📊 세 번째 마일스톤 달성
v2.0 작업 완료:
✅ 핫넘버/콜드넘버 분석 (최근 50회 vs 전체)
✅ 출현 간격 분석 (번호별 평균 간격)
✅ 장기 미출현 번호 추적 (44번 24회)
✅ 이동 평균 트렌드 (100회 윈도우)
✅ 당첨금 시계열 분석 (평균 23억)
✅ 상관관계 분석 (당첨금 vs 당첨자: -0.671)
✅ 연도별 추이 분석 (2014-2025)
흥미로운 발견
- 3번이 최근 폭발 (최근 50회에서 10회 출현, 20%)
- 44번이 24회 동안 미출현 (장기 미출현 1위)
- 이동 평균 트렌드와 실제 출현이 일치
- 당첨금과 당첨자 수의 음의 상관 (-0.671)
- 로또 당첨금도 인플레이션 반영 (47% 증가)
통계적 의미
핫넘버의 지속성:
- 3번: 최근 50회에서 10회 (20%)
- 확률적 기대값: 50 × (1/45) ≈ 1.1회
- 18배 이상 높은 출현율!
이건 우연일까?
→ 이항분포(Binomial Distribution)로 p-value 계산 시 p < 0.001 (매우 유의미)
하지만 주의:
- 로또는 독립 시행
- 과거가 미래를 보장하지 않음
- 단지 "최근 트렌드"일 뿐
🚀 다음 에피소드 예고
4편: "기계가 배우는 운의 법칙" - 머신러닝으로 번호 추천하기
다음 편에서는:
- 번호별 특징(Feature) 추출
- 점수 기반 랭킹 시스템 설계
- 연속 번호, 구간, 홀짝 패턴 학습
- 확률 가중치 기반 추천
- scikit-learn 없이 구현하는 ML
미리보기:
# prediction_model.py
def calculate_number_scores(self):
"""각 번호의 종합 점수 계산"""
for num in range(1, 46):
# 빈도 점수 (0-30점)
freq_score = min(total_frequency / 100 * 30, 30)
# 트렌드 점수 (0-30점)
trend_score = recent_50_frequency / 50 * 30
# 부재 기간 점수 (0-20점)
absence_score = min(absence_length / 20 * 20, 20)
# 핫넘버 점수 (0-20점)
hotness_score = min(hotness / 10 * 20, 20)
total = freq_score + trend_score + absence_score + hotness_score
# 최대 100점!
# 결과: 3번이 98.5점으로 1위!🔗 관련 링크
- GitHub: lotter645_1227
- Streamlit App: 로또 645 분석 웹 앱
- 이전 에피소드: 2편 - 숫자가 말을 걸 때
- 다음 에피소드: 4편 - 기계가 배우는 운의 법칙
💬 마무리하며
"시간은 흐르고, 데이터는 남는다."
3번이 최근 50회에서 10번 나왔다. 44번은 24회 동안 안 나왔다. 이동 평균을 따라가니 상승세와 하락세가 보였다.
당첨금도 시간과 함께 흘렀다. 2014년 평균 18.5억에서 2022년 27.2억으로 47% 증가했다. 로또도 인플레이션을 반영했다.
상관관계 분석은 의외의 발견을 주었다. 당첨자가 많을수록 당첨금이 줄어드는 건 당연하지만, 상관계수 -0.671이라는 구체적 수치가 주는 무게감이 달랐다.
박스플롯을 그리며 각 연도의 분포를 보았다. 2022년에 튀어나온 123억이라는 아웃라이어가 눈에 띄었다.
숫자는 시간 속에서 말을 걸었다. 이제 이 패턴들을 학습시켜 기계에게 번호를 추천받아보자. 머신러닝의 세계로 들어간다.
📌 SEO 태그
#포함 해시태그
#시계열분석 #핫넘버콜드넘버 #이동평균 #트렌드분석 #당첨금분석 #상관관계분석 #박스플롯 #NumPy통계 #Pandas시계열 #데이터트렌드
쉼표 구분 태그
시계열분석, 핫넘버, 콜드넘버, 이동평균, 트렌드, 출현간격, 미출현기간, 당첨금, 상관관계, 박스플롯, 연도별분석, 인플레이션
작성: @MyJYP
시리즈: 로또 645 데이터 분석 프로젝트 (3/10)
라이선스: CC BY-NC-SA 4.0
📊 Claude Code 사용량
작업 전:
- 세션 사용량: 57,094 tokens
작업 후:
- 세션 사용량: 67,052 tokens (84% 사용됨) 이미지 수정요청후 100% 사용함
사용량 차이:
- Episode 3 작성 사용량: 9,958 tokens (약 10K tokens)
- 주간 65%사용 (세션 제한에 걸림)
'VibeCoding > lo645251227' 카테고리의 다른 글
| Episode 1: 첫 줄의 코드, 605회의 시작 (The First Line: 605 Beginnings) (0) | 2026.01.11 |
|---|---|
| Episode 2: 숫자가 말을 걸 때 (When Numbers Speak) (0) | 2026.01.11 |
| Episode 4: 기계가 배우는 운의 법칙 (The Machine's Fortune: Learning Rules) (0) | 2026.01.11 |
| Episode 5: 일곱 가지 선택의 기로(Seven Choices, One Crossroad) (0) | 2026.01.11 |
| Episode 6: 브라우저에 피어난 분석 (Browser-Based Analysis) (1) | 2026.01.11 |